Assignment 2
目录
Question 1:
有一推销员, 从城市 $v_0$ 出发, 要依次访问城市 $v_1, v_2, \dots, v_n$ 各一次, 最后返回到 $v_0$. 已知从 $v_i$ 到 $v_j$ 的旅费为 $c_{ij}$, 对于任意的 $v_i$ 和 $v_j$, 问他应按怎样的次序访问这些城市, 使得总旅费最小?
答案
定义变量 $x_{ij}=\left\lbrace\begin{array}{ll}
1, & \text{路径中包含从} v_i\text{到} v_j \text{的边}\\
0, & \text{不包含}
\end{array}\right.$
那么我们的目标函数就是 $\min \sum\limits_{i,j=0}^n c_{ij}x_{ij}$.
接着考虑约束条件, 由于要用一条路径覆盖, 所以每个点只会有一个入边即 $\sum\limits_{i=0}^n x_{ij}=1$. 也只会有一条出边 $\sum\limits_{j=0}^n x_{ij}=1$.
但仍要保证路径是一条, 考虑加入辅助变量 $u_i, i=1,2,\ldots, n$, 只需满足 $u_i-u_j+x_{ij}(n)\leqslant n-1, i,j=1,2,\ldots,n$.
因为当 $1\sim n$ 中存在子连通图, 那么一定存在一个子环, 设大小, 而将这个环上的边 $(i,j)$ 对应的式子取出, 那么相加后所有的 $u_i,u_j$ 抵消, 左侧为 $kn$, 右侧为 $k(n-1)$ 显然不成立.
所以该限制确保了不存在子环. 而当只有一条路径时, 只需取 $u_i$ 表示第 i 个点的顺序即可保证所有等式成立, 因为此时 $1\leqslant u_i\leqslant n$, $u_i-u_j\leqslant n-1$ 成立.
故满足上述限制的解一定构成一条符合要求的路径. 汇总后可将模型写成.
$$\left\lbrace\begin{array}{lll} \min & z=\sum\limits_{i,j=0}^n c_{ij}x_{ij} &\\ \text{\ s.t.\ } & \sum\limits_{i=0}^{n}x_{ij}=1, & j=0,\ldots,n\\ & \sum\limits_{j=0}^n x_{ij}=1, & i=0,\ldots,n\\ & u_i-u_j+nx_{ij}\leqslant n-1, & 1\leqslant i,j \leqslant n. \\ & x_{ij}\in {0,1}, & i,j=0,\ldots,n\\ & u_i\in \mathbb{R} & i=1,\ldots,n \end{array}\right.$$
那么我们的目标函数就是 $\min \sum\limits_{i,j=0}^n c_{ij}x_{ij}$.
接着考虑约束条件, 由于要用一条路径覆盖, 所以每个点只会有一个入边即 $\sum\limits_{i=0}^n x_{ij}=1$. 也只会有一条出边 $\sum\limits_{j=0}^n x_{ij}=1$.
但仍要保证路径是一条, 考虑加入辅助变量 $u_i, i=1,2,\ldots, n$, 只需满足 $u_i-u_j+x_{ij}(n)\leqslant n-1, i,j=1,2,\ldots,n$.
因为当 $1\sim n$ 中存在子连通图, 那么一定存在一个子环, 设大小, 而将这个环上的边 $(i,j)$ 对应的式子取出, 那么相加后所有的 $u_i,u_j$ 抵消, 左侧为 $kn$, 右侧为 $k(n-1)$ 显然不成立.
所以该限制确保了不存在子环. 而当只有一条路径时, 只需取 $u_i$ 表示第 i 个点的顺序即可保证所有等式成立, 因为此时 $1\leqslant u_i\leqslant n$, $u_i-u_j\leqslant n-1$ 成立.
故满足上述限制的解一定构成一条符合要求的路径. 汇总后可将模型写成.
$$\left\lbrace\begin{array}{lll} \min & z=\sum\limits_{i,j=0}^n c_{ij}x_{ij} &\\ \text{\ s.t.\ } & \sum\limits_{i=0}^{n}x_{ij}=1, & j=0,\ldots,n\\ & \sum\limits_{j=0}^n x_{ij}=1, & i=0,\ldots,n\\ & u_i-u_j+nx_{ij}\leqslant n-1, & 1\leqslant i,j \leqslant n. \\ & x_{ij}\in {0,1}, & i,j=0,\ldots,n\\ & u_i\in \mathbb{R} & i=1,\ldots,n \end{array}\right.$$
Question 2:
需要将 11 件加工任务 (A-K) 分配到两个工作站, 任务需要依次经过工作站 1, 2 以完成加工. 任务间的依赖关系如下图 (后续节点任务的启动需要前序任务完成), 每件任务在工作站所花费的时间如下表:
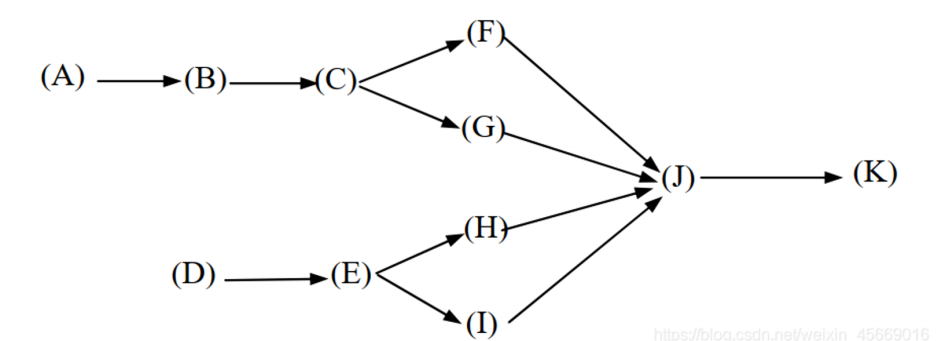
每件任务在两个工作站上所需时间如下表 (单位: 小时):
| 任务 | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 在工作站 1 上花费时间 (小时) | 25 | 5 | 5 | 35 | 10 | 7 | 8 | 7 | 2 | 4 | 7 |
| 在工作站 2 上花费时间 (小时) | 20 | 6 | 4 | 15 | 5 | 5 | 4 | 5 | 10 | 4 | 2 |
设计装配任务分配方案, 目标是为工作站分配加工任务, 尽可能使总装配时间最短.
答案
将 $A-K$ 对应到 $1-11$.
题目中的符号表示 $t_{ij}$ 表示第 $i$ 个任务在 $j$ 工作站上的耗时, 具体值见上表.
$P_i$ 表示任务 $i$ 的直接前序依赖任务集合, 例如 $P_{3}={2}$.
$M$ 为充分大的常数.
决策变量:
$x_i\in{0,1}$: 表示任务 $i$ 是否分配给工作站 $1$, $1$ 表示是, $0$ 表示否 ($i=1,\ldots,11$).
$S_i$ 表示任务 $i$ 的开工时间 ($i=1,\ldots,11$).
$y_{ij}\in{0,1}$ 表示任务 $i$ 是否在任务 $j$ 之前完成 ($i\neq j$).
为了方便, 先推导每个任务的结束时间记作 $C_i=S_i+x_it_{i1}+(1-x_i)t_{i2}$ 用 $x_i$ 控制在哪个工作站上.
目标函数:
$f=\min C_{11}$.
约束条件:
第一类是依赖关系, 即对于每个任务 $i$, 要求 $C_j\leqslant S_i,\forall j\in P_i$.
第二类是单个工作站上任务不重叠, 那么考虑先限定 $y_{ij}+y_{ji}=1$.
然后当 $x_i=x_j$ 时要求根据 $y_{ij}$ 的取值判断 $i,j$ 的先后顺序.
可以构建下面的条件
$$\left\lbrace\begin{array}{l} C_i\leqslant S_j+M(y_{ji}+2-x_i-x_j)\\ C_i\leqslant S_j+M(y_{ji}+x_i+x_j) \end{array}\right.$$
不难验证, 当 $x_i\neq x_j$ 时, 上述两个限制肯定成立. 而当 $x_i=x_j$ 时, 上述限制具有约束力, 仅当 $y_{ji}=0$, 即 $y_{ij}=1$. 此时要求 $i$ 在 $j$ 之前完成, 即 $C_i\leqslant S_j$. 满足定义.
所以只需对 $i\neq j$ 上述两条约束成立即可满足在单个工作站上不重叠.
综上, 汇总可得总的运筹模型可建立为
$$\left\lbrace\begin{array}{lll} \min & C_{11} & \\ \text{s.t.} & C_j\leqslant S_i & \forall j\in P_i, i=1,2,\ldots,11\\ & y_{ij}+y_{ji}=1 & 1\leqslant i\neq j\leqslant 11\\ & C_i\leqslant S_j+M(y_{ji}+2-x_i-x_j) & 1\leqslant i\neq j \leqslant 11 \\ & C_i\leqslant S_j+M(y_{ji}+x_i+x_j) & 1\leqslant i\neq j \leqslant 11\\ & x_{ij}\in {0,1} & 1\leqslant i\neq j\leqslant 11\\ & y_{ij}\in {0,1} & 1\leqslant i\neq j\leqslant 11\\ & C_i=S_i+x_i t_{i1}+(1-x_i)t_{i2} & i=1,\ldots,11\\ & S_i\geqslant 0 & i=1,\ldots,11 \end{array}\right.$$
下面是一组我得到的最优解, 并且分类讨论 A 一开始在 1,还是 2 可以证明该方案已经达到下界.
先简要证明.
如果 A 在工作站 1, 那么只考虑 A,B,C,F,G,J,K 这些任务, A 25h, B 最早 30h, C 最早 34h, F,G 最早 41h (F1G2), 再 J,K 依次完成最早要 47h.
如果 A 在工作站 2, 那么 D 最早在 35h 完成, E 最早 40h, H,I 最早 45h, 再 J,K 依次完成最早要 51h.
注意上述两种假设都忽略了部分任务以考虑最优, 所以实际必定不低于上述考虑, 所以总时间至少为 47h.
下面给出恰好为 47h 的方案.
在工作站 1 上依次完成 A,B,I,F.
在工作站 2 上依次完成 D,E,H,C,G,J,K.
几个重要的时间点,
$0\sim25h$ 工作站 1 完成 A, 工作站 2 完成 D,E,H.
$25\sim30h$ 工作站 1 完成 B, 工作站 2 等待.
$30\sim34h$ 工作站 1 完成 I, 工作站 2 完成 C.
$34\sim41h$ 工作站 1 完成 F, 工作站 2 完成 G.
接下来 6h 依次完成 J,K. 在 47h 时完成所有任务. 达到理论下界. 所以已经是最优解.
题目中的符号表示 $t_{ij}$ 表示第 $i$ 个任务在 $j$ 工作站上的耗时, 具体值见上表.
$P_i$ 表示任务 $i$ 的直接前序依赖任务集合, 例如 $P_{3}={2}$.
$M$ 为充分大的常数.
决策变量:
$x_i\in{0,1}$: 表示任务 $i$ 是否分配给工作站 $1$, $1$ 表示是, $0$ 表示否 ($i=1,\ldots,11$).
$S_i$ 表示任务 $i$ 的开工时间 ($i=1,\ldots,11$).
$y_{ij}\in{0,1}$ 表示任务 $i$ 是否在任务 $j$ 之前完成 ($i\neq j$).
为了方便, 先推导每个任务的结束时间记作 $C_i=S_i+x_it_{i1}+(1-x_i)t_{i2}$ 用 $x_i$ 控制在哪个工作站上.
目标函数:
$f=\min C_{11}$.
约束条件:
第一类是依赖关系, 即对于每个任务 $i$, 要求 $C_j\leqslant S_i,\forall j\in P_i$.
第二类是单个工作站上任务不重叠, 那么考虑先限定 $y_{ij}+y_{ji}=1$.
然后当 $x_i=x_j$ 时要求根据 $y_{ij}$ 的取值判断 $i,j$ 的先后顺序.
可以构建下面的条件
$$\left\lbrace\begin{array}{l} C_i\leqslant S_j+M(y_{ji}+2-x_i-x_j)\\ C_i\leqslant S_j+M(y_{ji}+x_i+x_j) \end{array}\right.$$
不难验证, 当 $x_i\neq x_j$ 时, 上述两个限制肯定成立. 而当 $x_i=x_j$ 时, 上述限制具有约束力, 仅当 $y_{ji}=0$, 即 $y_{ij}=1$. 此时要求 $i$ 在 $j$ 之前完成, 即 $C_i\leqslant S_j$. 满足定义.
所以只需对 $i\neq j$ 上述两条约束成立即可满足在单个工作站上不重叠.
综上, 汇总可得总的运筹模型可建立为
$$\left\lbrace\begin{array}{lll} \min & C_{11} & \\ \text{s.t.} & C_j\leqslant S_i & \forall j\in P_i, i=1,2,\ldots,11\\ & y_{ij}+y_{ji}=1 & 1\leqslant i\neq j\leqslant 11\\ & C_i\leqslant S_j+M(y_{ji}+2-x_i-x_j) & 1\leqslant i\neq j \leqslant 11 \\ & C_i\leqslant S_j+M(y_{ji}+x_i+x_j) & 1\leqslant i\neq j \leqslant 11\\ & x_{ij}\in {0,1} & 1\leqslant i\neq j\leqslant 11\\ & y_{ij}\in {0,1} & 1\leqslant i\neq j\leqslant 11\\ & C_i=S_i+x_i t_{i1}+(1-x_i)t_{i2} & i=1,\ldots,11\\ & S_i\geqslant 0 & i=1,\ldots,11 \end{array}\right.$$
下面是一组我得到的最优解, 并且分类讨论 A 一开始在 1,还是 2 可以证明该方案已经达到下界.
先简要证明.
如果 A 在工作站 1, 那么只考虑 A,B,C,F,G,J,K 这些任务, A 25h, B 最早 30h, C 最早 34h, F,G 最早 41h (F1G2), 再 J,K 依次完成最早要 47h.
如果 A 在工作站 2, 那么 D 最早在 35h 完成, E 最早 40h, H,I 最早 45h, 再 J,K 依次完成最早要 51h.
注意上述两种假设都忽略了部分任务以考虑最优, 所以实际必定不低于上述考虑, 所以总时间至少为 47h.
下面给出恰好为 47h 的方案.
在工作站 1 上依次完成 A,B,I,F.
在工作站 2 上依次完成 D,E,H,C,G,J,K.
几个重要的时间点,
$0\sim25h$ 工作站 1 完成 A, 工作站 2 完成 D,E,H.
$25\sim30h$ 工作站 1 完成 B, 工作站 2 等待.
$30\sim34h$ 工作站 1 完成 I, 工作站 2 完成 C.
$34\sim41h$ 工作站 1 完成 F, 工作站 2 完成 G.
接下来 6h 依次完成 J,K. 在 47h 时完成所有任务. 达到理论下界. 所以已经是最优解.
收录于 合集・运筹学作业 2