泛函分析作业251020
目录
1.4.9
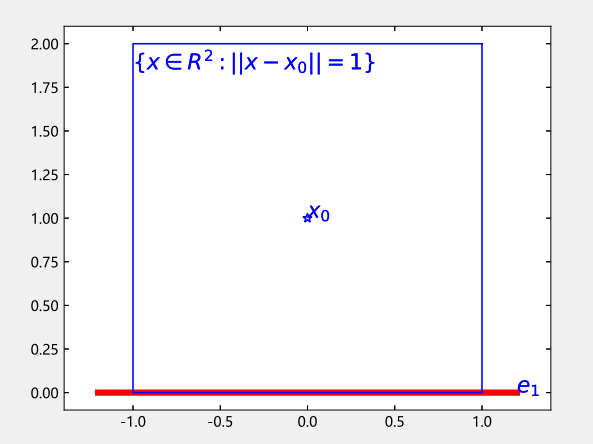
在 $\mathbb{R}^2$ 中, 对 $\forall x = (x_1, x_2) \in \mathbb{R}^2$, 定义范数
$$
\Vert x \Vert = \max(|x_1|, |x_2|),
$$
并设 $e_1 = (1, 0)$, $x_0 = (0, 1)$. 求 $a \in \mathbb{R}$ 适合
$$
\Vert x_0 - a e_1 \Vert = \min_{\lambda \in \mathbb{R}} \Vert x_0 - \lambda e_1 \Vert,
$$
并问这样的 $a$ 是否唯一? 请对结果做出几何解释.
答案
不唯一, $x_0-\lambda e_1$ 对应 $xOy$ 坐标系中 $y=1$ 的直线, 而在该范数定义下, $\Vert (a,1) \Vert =\begin{cases}
1,\quad a\in[-1,1] \\
|a|,\quad |a|>1
\end{cases}$ 于是当 $a\in[-1,1]$ 时均满足条件, 不唯一.
1,\quad a\in[-1,1] \\
|a|,\quad |a|>1
\end{cases}$ 于是当 $a\in[-1,1]$ 时均满足条件, 不唯一.
1.4.10
求证: 范数的严格凸性等价于下列条件:
$$
\Vert x + y \Vert = \Vert x \Vert + \Vert y \Vert \quad (\forall x \ne 0, y \ne 0) \implies x = c y \quad (c > 0).
$$
答案
“$\Rightarrow$”: 考虑 $\Vert x+y \Vert = \Vert \dfrac{x}{\Vert x \Vert} \Vert x \Vert + \dfrac{y}{\Vert y \Vert} \Vert y \Vert \Vert = (\Vert x \Vert + \Vert y \Vert) \Vert \dfrac{x}{\Vert x \Vert} \dfrac{\Vert x \Vert}{\Vert x \Vert + \Vert y \Vert} + \dfrac{y}{\Vert y \Vert} \dfrac{\Vert y \Vert}{\Vert x \Vert + \Vert y \Vert} \Vert$ 如果 $\dfrac{x}{\Vert x \Vert} \ne \dfrac{y}{\Vert y \Vert}$ 那么结合严格凸性可得 $\Vert x+y \Vert < \Vert x \Vert + \Vert y \Vert = \Vert x+y \Vert$ 矛盾, 所以 $\dfrac{x}{\Vert x \Vert} = \dfrac{y}{\Vert y \Vert}$ 即 $x = c y, (c > 0)$.
“$\Leftarrow$”: 首先范数一定是凸的, 故只需证明严格性. 反设存在 $x,y,\alpha,\beta$ 满足 $\Vert x \Vert = \Vert y \Vert = \alpha + \beta = 1, x \ne y$. 有 $\Vert \alpha x + \beta y \Vert = 1$. 那么有 $\Vert \alpha x + \beta y \Vert = 1 = \alpha \Vert x \Vert + \beta \Vert y \Vert \overset{\text{齐次性}}{=} \Vert \alpha x \Vert + \Vert \beta y \Vert$, 于是就有 $\alpha x = c \beta y$, 两边取范数立刻得到 $\alpha = c \beta$, 从而 $x = y$ 矛盾. 故该范数是严格凸的.
“$\Leftarrow$”: 首先范数一定是凸的, 故只需证明严格性. 反设存在 $x,y,\alpha,\beta$ 满足 $\Vert x \Vert = \Vert y \Vert = \alpha + \beta = 1, x \ne y$. 有 $\Vert \alpha x + \beta y \Vert = 1$. 那么有 $\Vert \alpha x + \beta y \Vert = 1 = \alpha \Vert x \Vert + \beta \Vert y \Vert \overset{\text{齐次性}}{=} \Vert \alpha x \Vert + \Vert \beta y \Vert$, 于是就有 $\alpha x = c \beta y$, 两边取范数立刻得到 $\alpha = c \beta$, 从而 $x = y$ 矛盾. 故该范数是严格凸的.
1.4.13
设 $\mathscr{X}$ 是 $B^*$ 空间, $\mathscr{X}_0$ 是 $\mathscr{X}$ 的线性子空间, 假定 $\exists c \in (0,1)$, 使得
$$
\inf_{x \in \mathscr{X}_0} \Vert y - x \Vert \le c \Vert y \Vert \quad (\forall y \in \mathscr{X}).
$$
求证: $\mathscr{X}_0$ 在 $\mathscr{X}$ 中稠密.
答案
反设 $\mathscr X_0$ 不稠密, 那么 $\overline{\mathscr X_0}$ 是 $\mathscr X$ 中的真闭子空间, 那么根据 Riesz 引理, 取 $\varepsilon = \frac{1 - c}{2}$, 那么存在 $y \in \mathscr X$, 使得 $\Vert y \Vert = 1$ 且 $\Vert y - x \Vert \geqslant 1 - \varepsilon > c = c \Vert y \Vert \ \forall x \in \mathscr X_0$ 这就与条件 $\inf \Vert y - x \Vert \leqslant c \Vert y \Vert$ 矛盾. 从而 $\mathscr X_0$ 在 $\mathscr X$ 中稠密.
1.4.14
设 $C_0$ 表示以 0 为极限的实数全体, 并在 $C_0$ 中赋以范数
$$
\Vert x \Vert = \max_{n \ge 1} |\xi_n| \quad (\forall x = (\xi_1, \xi_2, \cdots, \xi_n) \in C_0).
$$
又设
$$
M \triangleq \left\lbrace x = \lbrace \xi_n \rbrace_{n=1}^{\infty} \in C_0 \ \middle|\ \sum_{n=1}^{\infty} \frac{\xi_n}{2^n} = 0 \right\rbrace .
$$
- (1) 求证: $M$ 是 $C_0$ 的闭线性子空间.
- (2) 设 $x_0 = (2, 0, \cdots, 0, \cdots)$, 求证:
$$
\inf_{z \in M} \Vert x_0 - z \Vert = 1,
$$
但 $\forall y \in M$ 有 $\Vert x_0 - y \Vert > 1$.
答案
(1) 取映射 $f: C_0 \to \mathbb{R}, f(x) = \sum\limits_{n=1}^\infty \frac{\xi_n}{2^n}$
线性性: 考虑 $\alpha x + \beta y$: $f(\alpha x + \beta y) = \sum\limits_{n=1}^\infty \frac{\alpha \xi_n + \beta \eta_n}{2^n} = \alpha f(x) + \beta f(y) = 0$.
于是 $\alpha x + \beta y \in M$.
闭性: 由于 $|f(x)| \leqslant \sum\limits_{n=1}^\infty \frac{|\xi_n|}{2^n} \leqslant \Vert x \Vert \sum\limits_{n=1}^\infty \frac{1}{2^n} = \Vert x \Vert$.
所以 $f$ 是连续映射, 又 $\lbrace 0 \rbrace$ 是 $\mathbb{R}$ 中的闭集, 所以 $M = f^{-1}(\lbrace 0 \rbrace)$ 是闭集.
故 $M$ 是 $C_0$ 的闭线性子空间.
(2) 考虑第一项有 $\Vert x_0 - z \Vert \geqslant \max \lbrace |2 - \xi_1|, |\xi| \rbrace \geqslant 1$. 所以 $\inf\limits_{z \in M} \Vert x_0 - z \Vert = 1$.
考虑数列 $x^N = (1 - \frac{1}{2^{N-1}}, \underbrace{-1, \ldots, -1}_{N\ \text{个}}, 0, \ldots, 0, \ldots) \in M$, 有 $\Vert x_0 - x^N \Vert = 1 + \frac{1}{2^{N-1}}$, 所以下确界取到 1. $\inf\limits_{z \in M} \Vert x_0 - z \Vert = 1$.
下证 $\forall y \in M$ 有 $\Vert x_0 - y \Vert > 1$.
考虑反证法, 假设存在序列 $y = (\xi_1, \xi_2, \ldots, \xi_k, \ldots) \in M$, 使得 $\Vert x_0 - y \Vert = 1$, 则有 $$\begin{cases}
|\xi_k| \leqslant 1, & k \geqslant 2, \\
2 - \xi_1 \leqslant 1. &
\end{cases}$$
所以有 $$\left| \sum\limits_{k=2}^\infty \frac{\xi_k}{2^k} \right| \leqslant \sum\limits_{k=2}^\infty \frac{|\xi_k|}{2^k} \overset{\text{由极限为 0 不可能一直是 1}}{<} \sum\limits_{k=2}^\infty \frac{1}{2^k} = \frac{1}{2}.$$
$$\Rightarrow \left| \frac{\xi_1}{2} \right| = \left| \sum\limits_{k=2}^\infty \frac{\xi_k}{2^k} \right| < \frac{1}{2} \Rightarrow |\xi_1| < 1.$$ 这与 $|2 - \xi_1| \leqslant 1$ 矛盾.
所以有 $\forall y \in M$ 有 $\Vert x_0 - y \Vert > 1$.
线性性: 考虑 $\alpha x + \beta y$: $f(\alpha x + \beta y) = \sum\limits_{n=1}^\infty \frac{\alpha \xi_n + \beta \eta_n}{2^n} = \alpha f(x) + \beta f(y) = 0$.
于是 $\alpha x + \beta y \in M$.
闭性: 由于 $|f(x)| \leqslant \sum\limits_{n=1}^\infty \frac{|\xi_n|}{2^n} \leqslant \Vert x \Vert \sum\limits_{n=1}^\infty \frac{1}{2^n} = \Vert x \Vert$.
所以 $f$ 是连续映射, 又 $\lbrace 0 \rbrace$ 是 $\mathbb{R}$ 中的闭集, 所以 $M = f^{-1}(\lbrace 0 \rbrace)$ 是闭集.
故 $M$ 是 $C_0$ 的闭线性子空间.
(2) 考虑第一项有 $\Vert x_0 - z \Vert \geqslant \max \lbrace |2 - \xi_1|, |\xi| \rbrace \geqslant 1$. 所以 $\inf\limits_{z \in M} \Vert x_0 - z \Vert = 1$.
考虑数列 $x^N = (1 - \frac{1}{2^{N-1}}, \underbrace{-1, \ldots, -1}_{N\ \text{个}}, 0, \ldots, 0, \ldots) \in M$, 有 $\Vert x_0 - x^N \Vert = 1 + \frac{1}{2^{N-1}}$, 所以下确界取到 1. $\inf\limits_{z \in M} \Vert x_0 - z \Vert = 1$.
下证 $\forall y \in M$ 有 $\Vert x_0 - y \Vert > 1$.
考虑反证法, 假设存在序列 $y = (\xi_1, \xi_2, \ldots, \xi_k, \ldots) \in M$, 使得 $\Vert x_0 - y \Vert = 1$, 则有 $$\begin{cases}
|\xi_k| \leqslant 1, & k \geqslant 2, \\
2 - \xi_1 \leqslant 1. &
\end{cases}$$
所以有 $$\left| \sum\limits_{k=2}^\infty \frac{\xi_k}{2^k} \right| \leqslant \sum\limits_{k=2}^\infty \frac{|\xi_k|}{2^k} \overset{\text{由极限为 0 不可能一直是 1}}{<} \sum\limits_{k=2}^\infty \frac{1}{2^k} = \frac{1}{2}.$$
$$\Rightarrow \left| \frac{\xi_1}{2} \right| = \left| \sum\limits_{k=2}^\infty \frac{\xi_k}{2^k} \right| < \frac{1}{2} \Rightarrow |\xi_1| < 1.$$ 这与 $|2 - \xi_1| \leqslant 1$ 矛盾.
所以有 $\forall y \in M$ 有 $\Vert x_0 - y \Vert > 1$.
注
本题提供一个例子说明: 对于无穷维闭线性子空间来说, 给定其外一点 $x_0$, 未必能在其上找到一点 $y$ 适合
$$
\Vert x_0 - y \Vert = \inf_{z \in M} \Vert x_0 - z \Vert.
$$
换句话说, 给定 $x_0 \notin M$, 未必能在 $M$ 上找到最佳逼近元.
$$
\Vert x_0 - y \Vert = \inf_{z \in M} \Vert x_0 - z \Vert.
$$
换句话说, 给定 $x_0 \notin M$, 未必能在 $M$ 上找到最佳逼近元.
1.4.17
设有商空间 $\mathscr{X} / \mathscr{X}_0$.
- (1) 设 $[x] \in \mathscr{X} / \mathscr{X}_0$, 求证: 对 $\forall x \in [x]$, 有
$$
\inf_{z \in \mathscr{X}_0} \Vert x - z \Vert = \Vert [x] \Vert_0.
$$ - (2) 定义映射 $\varphi : \mathscr{X} \to \mathscr{X} / \mathscr{X}_0$ 为
$$
\varphi(x) = [x] \triangleq x + \mathscr{X}_0 \quad (\forall x \in \mathscr{X}),
$$
求证: $\varphi$ 是连续线性映射. - (3) $\forall [x] \in \mathscr{X} / \mathscr{X}_0$, 求证: $\exists x \in \mathscr{X}$, 使得
$$
\varphi(x) = [x], \quad \text{且} \quad \Vert x \Vert \le 2 \Vert [x] \Vert_0.
$$ - (4) 设 $\mathscr{X} = C[0,1]$, $\mathscr{X}_0 = \lbrace f \in \mathscr{X} \mid f(0) = 0 \rbrace$, 求证:
$$
\mathscr{X} / \mathscr{X}_0 \cong \mathbb{K},
$$
其中记号 “$\cong$” 表示等距同构.
答案
- (1) $\Vert [x] \Vert = \inf\limits_{y \in [x]} \Vert y \Vert = \inf\limits_{y \in \mathscr X_0} \Vert x + y \Vert = \inf\limits_{z \in \mathscr X_0} \Vert x - z \Vert$.
- (2) 根据商空间运算定义, 线性性显然. $\Vert \varphi(x) \Vert_0 = \inf\limits_{z \in \mathscr X_0} \Vert x - z \Vert \leqslant \Vert x - 0 \Vert = \Vert x \Vert$ 所以 $\varphi(x)$ 连续.
- (3) 取代表元 $x’$, 根据 $\Vert [x] \Vert_0 = \inf\limits_{z \in \mathscr X_0} \Vert x’ - z \Vert$ 所以对任意 $\varepsilon > 0$, 存在 $z \in \mathscr X_0$ 使得 $\Vert x’ - z \Vert < \Vert [x] \Vert_0 + \varepsilon$, 现取 $\varepsilon = \Vert [x] \Vert_0$, 则 $x’ + z_0$ 满足 $\varphi(x’) = [x],\ \Vert x \Vert \leqslant 2 \Vert [x] \Vert_0$.
- (4) 取 $T: \mathscr X / \mathscr X_0 \to \mathbb K, T([f]) = f(0)$. 首先先探究等价类的性质, 若 $f - g \in \mathscr X_0$, 那么有 $f(0) = g(0)$, 所以我们不妨设等价类为 $[f_x]$ 表示所有 $f(0) = x$ 的函数.
先证 $T$ 是线性映射, 即 $T(\alpha [f_x] + \beta [f_y]) = T([f_{\alpha x} + f_{\beta y}]) = \alpha x + \beta y = \alpha T([f_x]) + \beta T([f_y])$. 这一步用到了 $\mathbb{K}$ 的线性性.
再证 $T$ 保范数, 即要证 $\Vert T([f_x]) \Vert = \Vert x \Vert$.
根据定义取 $[f_x]$ 的代表元为 $f,\ f(0) = x$, 有 $\Vert T([f_x]) \Vert = \inf\limits_{g \in \mathscr X_0} \Vert f - g \Vert = \inf\limits_{g \in \mathscr X_0} \max\limits_{t \in [0,1]} |f(t) - g(t)|$
一方面, $$\inf\limits_{g \in \mathscr X_0} \max\limits_{t \in [0,1]} |f(t) - g(t)| \geqslant \inf\limits_{g \in \mathscr X_0} |f(0) - g(0)| = |x|$$
另一方面, 取 $g’ = f - x \in \mathscr X_0$, 从而 $$\inf\limits_{g \in \mathscr X_0} \Vert f - g \Vert \leqslant \Vert f - g’ \Vert \overset{\text{恒为 x 的常函数}}{=} \Vert x \Vert,$$ 所以有 $\Vert T([f_x]) \Vert = \Vert x \Vert$.
注
注意区分上述过程中的范数具体含义.