泛函分析作业251008
1.4.1
在二维空间 $\mathbb{R}^2$ 中, 对每一点 $z = (x, y)$, 令 $$ |z|_1 = |x| + |y|; \quad |z|_2 = \sqrt{x^2 + y^2}; \quad |z|_3 = \max(|x|, |y|); \quad |z|_4 = (x^4 + y^4)^{\frac{1}{4}}. $$
(1) 求证 $|\cdot|_i$ ($i=1,2,3,4$) 都是 $\mathbb{R}^2$ 的范数.
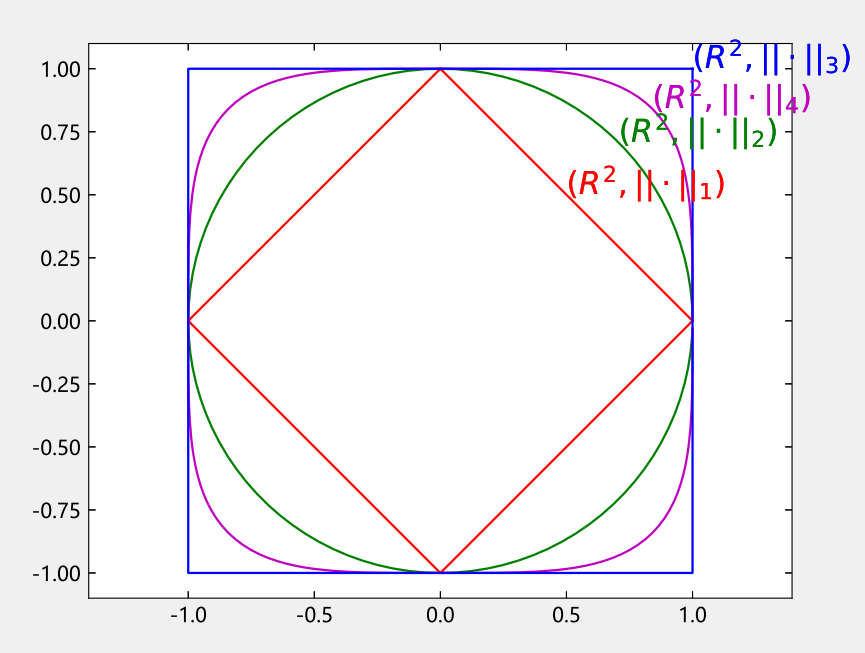
(2) 画出 $(\mathbb{R}^2, |\cdot|_i)$ ($i=1,2,3,4$) 各空间中的单位球面图形.
(3) 在 $\mathbb{R}^2$ 中取定三点 $O = (0,0)$, $A = (1,0)$, $B = (0,1)$, 试在上述四种不同范数下求出 $\triangle OAB$ 三边的长度.
(1) 正定性: 显然四者都是非负的, 并且当且仅当 $z=(0,0)$ 时为 0.
齐次性: $\Vert\alpha z\Vert_1=|\alpha x|+|\alpha y|=\alpha\Vert z_1\Vert$,
$\Vert\alpha z\Vert_2=\sqrt{(\alpha x)^2+(\alpha y)^2}=\alpha\sqrt{x^2+y^2}=\alpha\Vert z\Vert_2$,
$\Vert\alpha z\Vert_3=\max(|\alpha x|,|\alpha y|)=\alpha\max(|x|,|y|)=\alpha\Vert z\Vert_3$,
$\Vert\alpha z\Vert_4=((\alpha x)^4+(\alpha y)^4)^{1/4}=\alpha (x^4+y^4)^{1/4}=\alpha\Vert z\Vert_4$.
三角不等式:
$\Vert z_1+z_2\Vert_1=|x_1+x_2|+|y_1+y_2|\leqslant |x_1|+|x_2|+|y_1|+|y_2|=\Vert z_1\Vert_1+\Vert z_2\Vert_1$,
$\Vert z_1+z_2\Vert_2=\sqrt{(x_1+x_2)^2+(y_1+y_2)^2}\leqslant \sqrt{x_1^2+y_1^2}+\sqrt{x_2^2+y_2^2}=\Vert z_1\Vert_2+\Vert z_2\Vert_2$,
$\Vert z_1+z_2\Vert_3=\max(|x_1+x_2|,|y_1+y_2|)\leqslant \max(|x_1|,|y_1|)+\max(|x_2|,|y_2|)=\Vert z_1\Vert_3+\Vert z_2\Vert_3$,
$\Vert z_1+z_2\Vert_4=((x_1+x_2)^4+(y_1+y_2)^4)^{1/4}\leqslant (x_1^4+y_1^4)^{1/4}+(x_2^4+y_2^4)^{1/4}=\Vert z_1\Vert_4+\Vert z_2\Vert_4$.
(2)
(3)
$\Vert\cdot\Vert_1: 4$, $\Vert\cdot\Vert_2: 2+\sqrt{2}$, $\Vert\cdot\Vert_3: 3$, $\Vert\cdot\Vert_4: 2+\sqrt[4]{2}$.
1.4.2
设 $C(0,1]$ 表示 $(0,1]$ 上连续且有界的函数 $x(t)$ 全体. 对 $\forall x \in C(0,1]$, 令 $|x\Vert = \sup_{0 < t \leqslant 1} |x(t)|$. 求证:
(1) $|\cdot|$ 是 $C(0,1]$ 上的范数;
(2) $l^\infty$ 与 $C(0,1]$ 的一个子空间是等距同构的.
(1) 正定性显然.
齐次性 $\Vert\alpha x(t)\Vert=\sup_{0<t\leqslant 1}|\alpha x(t)|=\alpha\sup_{0<t\leqslant 1}|x(t)|=\alpha\Vert x(t)\Vert$.
三角不等式:
$\Vert x_1(t)+x_2(t)\Vert=\sup_{0<t\leqslant 1}|x_1(t)+x_2(t)|\leqslant \sup|x_1(t)|+\sup|x_2(t)|=\Vert x_1(t)\Vert+\Vert x_2(t)\Vert$.
(2) 构造映射 $T: l^\infty\to C(0,1]$, $\forall {a_n}\in l^\infty$,
$T({a_n})$ 表示 $x(\frac1n)=a_n$ 且用折线段连接 $x(\frac 1n),x(\frac1{n+1})$ 两点的连续函数.
显然这是个单射且像集是 $C(0,1]$ 的子集. 并且该映射是线性映射.
下面证其还保范数: 对折线段, 其最大值取在端点处, 故
$\Vert T({a_n})\Vert=\sup x(\frac 1 n)=\sup a_n=\Vert{a_n}\Vert$.
所以 $l^\infty$ 与 $C(0,1]$ 的一个子空间 $T(l^\infty)$ 等距同构.
1.4.3
在 $C^1[a,b]$ 中, 令
$$
|f|_1 = \left( \int_a^b (|f|^2 + |f’|^2) , \text{d}x \right)^{\frac{1}{2}} \quad (\forall f \in C^1[a,b]),
$$
(1) 求证 $|\cdot|_1$ 是 $C^1[a,b]$ 上的范数.
(2) 问 $(C^1[a,b], |\cdot|_1)$ 是否完备?
(1) 正定性由连续函数性质可知. 齐次性由积分线性性可知.
三角不等式: 用柯西施瓦茨不等式可得
$\int_a^b |fg|+|f’g’|\text{d}x\leqslant \Vert f\Vert_1\Vert g\Vert_1$.
(2) 任取 $c\in (a,b)$, 对 $f(x)=|x-c|\notin C^1[a,b]$,
但函数列 $f_n(x)=\sqrt{(x-c)^2+\frac 1n}$.
有 $|f_n(x)-f(x)|\leqslant\sqrt{\frac1n}$, 故 $\int_a^b |f_n-f|^2\text{d}x\leqslant (b-a)\frac1n$.
考虑 $sgn_c(x)=\left\lbrace\begin{array}{ll} -1,& x<c\\ 0, & x=c\\ 1, & x>c \end{array}\right.$
有 $|f_n’(x)-sgn_c(x)|=|(x-c)|(\frac{1}{|x-c|}-\frac{1}{\sqrt{(x-c)^2+\frac 1 n}})$.
从而 $\Vert f_n-f\Vert=O(\frac{1}{\sqrt n})\to 0$,
即 ${f_n}$ 收敛至 $f$, 但 $f\notin C^1[a,b]$, 故不完备.
1.4.4
在 $C[0,1]$ 中, 对每一个 $f \in C[0,1]$, 令
$$
|f|_1 = \left( \int_0^1 |f(x)|^2 , \text{d}x \right)^{\frac{1}{2}}, \quad
|f|_2 = \left( \int_0^1 (1+x) |f(x)|^2 , \text{d}x \right)^{\frac{1}{2}}.
$$
求证: $\Vert\cdot\Vert_1$ 和 $\Vert\cdot\Vert_2$ 是 $C[0,1]$ 中的两个等价范数.
$\Vert f\Vert_1\leqslant\Vert f\Vert_2\leqslant\sqrt{2}\Vert f\Vert_1$.
1.4.5
设 $BC[0,\infty)$ 表示 $[0,\infty)$ 上连续且有界的函数 $f(x)$ 全体, 对每个 $f \in BC[0,\infty)$ 及 $a > 0$, 定义 $$ |f|_a = \left( \int_0^\infty e^{-ax} |f(x)|^2 , \text{d}x \right)^{\frac{1}{2}}. $$
(1) 求证 $|\cdot|_a$ 是 $BC[0,\infty)$ 上的范数.
(2) 若 $a, b > 0$, $a \neq b$, 求证 $|\cdot|_a$ 与 $|\cdot|_b$ 不等价.
(1) 正定性: 若 $f\neq 0$, 则 $\Vert f\Vert_a\neq 0$.
齐次性:
$\Vert\alpha f\Vert=\left(\displaystyle\int_0^\infty e^{-ax}|\alpha f(x)|^2\text{d}x\right)^{1/2}
=\alpha\Vert f\Vert_a$.
三角不等式:
由柯西-施瓦茨不等式,
$\int_0^\infty e^{-ax}|f+g|^2\text{d}x\leqslant(\Vert f\Vert_a+\Vert g\Vert_a)^2$.
(2) 不妨设 $a>b>0$, 考虑函数列 $f_n(x)=\begin{cases} 0,&x\in[0,n-\frac1b]\\ be^{bn}(x-n+\frac1b),&x\in(n-\frac1b,n]\\ e^{bx},&x\in(n,n+1]\\ e^{b(n+1)}-(x-n-1)be^{b(n+1)},&x\in(n+1,n+1+\frac1b)\\ 0,&x\geqslant n+1+\frac1b \end{cases}$
在 $\Vert\cdot\Vert_a$ 中, $\Vert f_n\Vert_a\leqslant \displaystyle\int_{n-\frac1b}^{n+1+\frac1b}e^{(b-a)x}\text{d}x\leqslant \frac{1}{a-b}e^{(b-a)(n-\frac1b)}\to0$.
但在 $\Vert\cdot\Vert_b$ 中, $\Vert f_n\Vert_b\geqslant \displaystyle\int_n^{n+1}e^{bx-bx}\text{d}x=1$,
从而两个范数不等价.
1.4.8
记 $[a,b]$ 上次数不超过 $n$ 的多项式全体为 $\mathbb{P}_n$. 求证: $\forall f(x) \in C[a,b], \exists P_0(x) \in \mathbb{P}_n$, 使得 $$ \max_{a \leqslant x \leqslant b} |f(x) - P_0(x)| = \min_{P \in \mathbb{P}_n} \max_{a \leqslant x \leqslant b} |f(x) - P(x)|. $$ 即 $P_0(x)$ 是对 $f(x)$ 的最佳一致逼近.
$\mathbb P_n$ 是有限维子空间, 故根据最佳逼近元定理,
存在唯一的 $P_0(x)\in\mathbb P_n$ 使得
$\Vert P_0-f\Vert=\rho(f,\mathbb P_n)$.