泛函分析作业250915
1.1.2
(Newton 法) 设 $f$ 是定义在 $[a,b]$ 上的二次连续可微的实值函数, $\hat{x}\in(a,b)$ 使得 $f(\hat x)=0, f’(\hat x)\neq 0$. 求证: 存在 $\hat x$ 的邻域 $U(\hat x)$, 使得 $\forall x_0\in U(\hat x)$, 迭代序列 $$x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}\quad (n=0,1,2,\ldots)$$ 是收敛的, 并且 $$\lim\limits_{n\to\infty}x_n=\hat x.$$
设映射 $T(x)=x-\dfrac{f(x)}{f’(x)}$
由 $f\in C^2, f’(\hat x)\neq 0$, 故存在 $\delta_0, (x-\delta_0,x+\delta_0)\subset[a,b],m,M,L\in\mathbb{R},\ s.t.\ |x-\hat x|\leqslant \delta_0$ 时, 有 $m\overset{\text{保号性}}{\leqslant}|f’(x)|\overset{\text{有界性}}{\leqslant} M, |f’’(x)|\leqslant L$.
那么考虑导数 $T’(x)=\dfrac{f(x)f’’(x)}{(f’(x))^2}\overset{\text{柯西中值}}{=}\dfrac{(f’(\xi)|x-\hat x|+f(\hat x))f’’(x)}{(f’(x))^2}\leqslant \dfrac{M|x-\hat{x}|L}{m^2}$, 于是可以取 $\delta=\min(\frac {m^2}{ML+1},\delta_0)$, 则有 $|T’(x)|\leqslant \frac{ML}{ML+1}<1,\forall x\in (\hat x-\delta,\hat x+\delta)$.
所以在该邻域中有 $|T(x)-T(y)|\leqslant \frac{ML}{ML+1}|x-y|,\ \forall x,y\in (\hat x-\delta,\hat x+\delta)$, 再结合 $T(\hat{x})=\hat x$ 可以得到 $T x\in(\hat x-\delta,\hat x+\delta)$, 即 $T$ 在该邻域内是压缩映射.
又由实数的完备性, 根据 Banach 不动点定理可知存在唯一的不动点, 又 $\hat x=T(\hat x)$, 所以 $\hat x$ 是不动点, 即 $\lim\limits_{n\to\infty}x_n=\hat x$.
下面是 Mworks 程序.
1clear()
2clc()
3
4f(x)=exp.(x).-2 #求此函数的零点
5df(x)=exp.(x) #此函数的导数
6
7#绘制f的函数图像
8t=0:0.1:1.1
9plot(t,f(t),"k")
10hold("on")
11
12#绘制直线y=0
13plot(t,zeros(size(t)),"r")
14
15x0=0 #初始猜测
16N=3 #总迭代次数
17x=zeros(1,N+1)
18x[1]=x0;
19for ii=1:N
20x[ii+1]=x[ii]-f(x[ii])/df(x[ii])
21text(x[ii],f(x[ii]),string(ii-1),color="black",fontsize=14)
22plot(x[ii:ii+1],f(x[ii:ii+1]),"b")
23plot(x[ii+1],f(x[ii+1]),"r*")
24end
25text(x[N+1],f(x[N+1]),string(N),color="black",fontsize=14)
26saveas(gcf(),"1d1d2.eps")
27[x;
28abs.(x.-log(2))] #零点为log(2)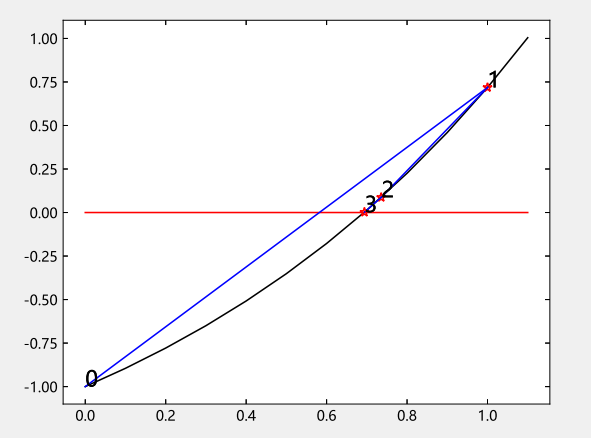
1.1.4
设 $T$ 是度量空间上的压缩映射, 求证: $T$ 是连续的.
记度量空间为 $(\mathscr X,\rho)$.
设 ${x_n}_{n=1}^\infty$ 是该度量空间上的任意收敛列, 且收敛至 $x_0$. 那么对于 $\rho(Tx_n,Tx_0)$, 由于 $T$ 是压缩映射, 故存在 $0<\alpha<1$ 满足 $\rho(Tx,Ty)\leqslant\alpha\rho(x,y),\ \forall x,y\in\mathscr X$, 于是 $0\leqslant\rho(Tx_n,Tx_0)\leqslant\alpha\rho(x_n,x_0)$, 根据夹逼准则可知 $\rho(Tx_n,Tx_0)\to 0\ (n\to \infty)$, 所以 $T$ 是连续的.
1.1.5
设 $T$ 是压缩映射, 求证: $T^n(n\in\mathbb{N}_+)$ 也是压缩映射, 并说明逆命题不一定成立.
记度量空间为 $(\mathscr X,\rho)$.
由 $T$ 是压缩映射, 所以存在 $0<\alpha<1$, 满足 $\rho(Tx,Ty)\leqslant\alpha\rho(x,y),\ \forall x,y\in \mathscr X$. 于是有 $$\rho(T^n x,T^n y)\leqslant\alpha\rho(T^{n-1}x,T^{n-1}y)\leqslant\cdots\leqslant\alpha^n\rho(x,y).$$ 由于 $0<\alpha<1$, 故 $0<\alpha^n<1$. 又 $T$ 将 $\mathscr X$ 映到自身, 因此 $T^n$ 也将 $\mathscr X$ 映到自身. 综上可知 $T^n$ 仍为压缩映射。
逆命题不一定成立, 下面给出一个反例:
在 $[0,1)$ 上以普通绝对值作度量, 取映射 $T(x)=\dfrac{1+\sqrt{3}}{6}x^3$。
显然 $T$ 将 $[0,1)$ 映到 $[0,1)$。
计算导数得 $T’(x)=\dfrac{1+\sqrt{3}}{2}x^2$, 存在 $x$ 使得 $T’(x)>1$, 因此 $T$ 不是压缩映射。
但是由链式法则, $$ (T^2(x))’ = T’(T(x))\cdot T’(x) = \frac{(1+\sqrt 3)^4}{144} x^8 <1,\quad \forall x\in[0,1),$$ 因此 $T^2$ 是压缩映射。
注: 上述构造的思路是考虑幂函数 $T(x)=c x^k$, 通过对系数 $c$ 和次幂 $k$ 的选择可以令 $T’$ 在某些点大于 1 而 $T^2$ 的导数处处小于 1,从而构成逆命题不成立的反例。
1.1.6
设 $M$ 是 $(\mathbb{R}^n,\rho)$ 中的有界闭集, 映射 $T:M\to M$ 满足: $\rho(Tx,Ty)<\rho(x,y)(\forall x,y\in M,x\neq y)$, 求证: $T$ 在 $M$ 中存在唯一的不动点.
由 $\rho(Tx,Ty)<\rho(x,y)$ 和三角不等式可得 $$|\rho(x,Tx)-\rho(y,Ty)|\leqslant \rho(x,y)+\rho(Tx,Ty)<2\rho(x,y),$$ 从而 $\rho(x,Tx)$ 是连续的。
由于 $M$ 是 $\mathbb{R}^n$ 中的有界闭集, 因此存在使 $\rho(x,Tx)$ 取得最小值的点 $x_0\in M$. 若 $\rho(x_0,Tx_0)=0$ 则 $x_0$ 为不动点。
若 $\rho(x_0,Tx_0)>0$, 则由假设有 $\rho(Tx_0,T^2x_0)<\rho(x_0,Tx_0)$, 即 $Tx_0$ 的值更小,这与 $x_0$ 为最小值点矛盾。因此必须有 $\rho(x_0,Tx_0)=0$,即存在不动点。
唯一性则与压缩映像原理一致:若存在两个不动点 $x_0,x_1$,则 $$\rho(x_0,x_1)=\rho(Tx_0,Tx_1)<\rho(x_0,x_1),$$ 矛盾。因此不动点唯一。
注: 在度量空间中关于连续性的论证要以度量 $\rho$ 为度量依据,即在选取 $\delta$ 时是针对 $\rho(x,x’)$ 的限制,注意区分欧式距离上的连续性与一般度量空间中的连续性的表述。
1.1.7
对于积分方程 $$x(t)-\lambda\int_0^1 e^{t-s}x(s)\text{d} s=y(t),$$ 其中 $y(t)\in C[0,1]$ 为给定函数, $\lambda$ 为常数, $|\lambda|<1$, 求证: 存在唯一解 $x(t)\in C[0,1]$.
考虑度量 $\rho(f,g)=\max\limits_{t\in[0,1]}|f(t)-g(t)|$.
对积分方程做变换得到 $e^{-t}x(t)-\lambda\int_0^1 e^{-s}x(s)\text{d} s=e^{-t}y(t)$.
不妨设 $\varphi(t)=e^{-t}x(t),\ \psi(t)=e^{-t}y(t)$, 新的函数显然仍属于 $C[0,1]$, 那么方程变为 $$\varphi(t)=\lambda\int_0^1 \varphi(s)\text{d} s+\psi(t).$$
考虑映射 $T(\varphi)=\psi+\lambda\int_0^1 \varphi\text{d} s$。
首先, 由 $\psi\in C[0,1]$, 所以 $T(\varphi)\in C[0,1]$, 映射到自身。
其次, 对于任意两个属于 $C[0,1]$ 的函数 $f,g$ 有
$$\rho(Tf,Tg)=\lambda\int_0^1 |f(t)-g(t)|\text{d} t\leqslant\lambda\max\limits_{t\in[0,1]}|f(t)-g(t)|=\lambda\rho(f,g).$$
由于 $|\lambda|<1$, 可知 $T$ 是压缩映射, 因此由压缩映像原理可得方程有唯一解. 乘以 $e^{t}$ 的变换是双射, 故原方程在 $C[0,1]$ 上也有唯一解。
下面是 Mworks 程序.
clear()
clc()
n=20; #离散节点总数
t=1/(2*n):1/n:1-1/(2*n) #居中节点
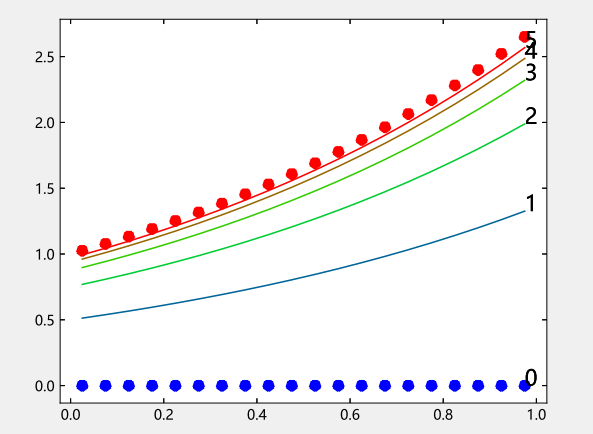
iter=5 #总迭代次数
x=zeros(n,iter+1)
plot(t,x[:,1],"b*",linewidth=4) #绘制初始猜测(蓝色点)
hold("on")
text(t[end],x[end,1],string(0),color="black",fontsize=14)
lambda=0.5
y=(1-lambda).*exp.(t)
for ii=1:iter
x[:,ii+1]=lambda/n*exp.(t .- transpose(t))*x[:,ii]+y
color_value=2*ii/iter-1 #取值范围调整为-1 到 1, 为使线段颜色可以rgb插值渐变
if color_value>0
plot(t,x[:,ii+1],color=[color_value,1-color_value,0]) #绘制此步结果
else
plot(t,x[:,ii+1],color=[0,1+color_value,-color_value]) #绘制此步结果
end
text(t[end],x[end,ii+1],string(ii),color="black",fontsize=14)
end
x_true=exp.(t)
plot(t,x_true,"r*",linewidth=4) #绘制精确结果(红色点)
saveas(gcf(),"1d1d7.eps")
[x x_true]