lgr118

uuku 收录于算法竞赛

2025-01-08 约 1600 字预计阅读 8 分钟

PMTD

设当前的最大值为 $mx$，最小值为 $mn$。为了让极差变大，我们显然是只操作这两个数。并且一定是让 $mx$ 变大，$mn$ 变小。

所以我们只可能进行这四个操作：

$mx:=mx+2$。
$mx:=mx\times 2$。
$mn:=mn-2$。
$mn:=\lfloor \dfrac {mn}{2}\rfloor$。

下面我们就来考虑那种操作对答案的贡献更大：

设一次操作对答案的贡献为 $dlt$。

那么这四种操作的贡献分别为：

$dlt_1=2$。
$dlt_2=mx$。
$dlt_3=2$。
$dlt_4=mn-\lfloor \dfrac{mn}{2}\rfloor$。

显然有 $dlt_4\le mn \le mx=dlt_2$。所以操作 $4$ 不可能进行。也就意味着如果我们改变最小值，每次操作最多将答案 $+2$。而如果改变最大值，每次操作至少可以让答案 $+2$。所以我们只要操作最大值就可以了。

下面我们考虑如何选取 $1$ 和 $2$ 操作。

不难发现，当 $mx>2$ 时，进行 $2$ 操作更优。当 $mx=2$ 时，两种操作效果一样。当 $mx<2$ 时，进行 $1$ 操作更优。

并且当进行一次 $1$ 操作后必然有 $mx\ge2$。

所以我们只需要记录初始序列的最大值和最小值，如果最大值小于 $2$，就先将其 $+2$，然后不断的对最大值进行 $\times 2$ 操作即可。

下面是 $\text{std}$：

 1#include<cstdio>
 2int n,val,mx,mn=1e9,m;
 3int main()
 4{
 5	scanf("%d%d",&n,&m);
 6	while(n--)
 7	{
 8		scanf("%d",&val);
 9		if(val>mx)mx=val;
10		if(val<mn)mn=val;
11	}
12	if(mx<2)mx+=2,m--;
13	printf("%lld",((1ll*mx)<<m)-mn);
14	return 0;
15}

Number

先考虑如何分配使乘积最大。

最优构造：按照从9到1的顺序将每个数字依次加入a,b两个数中，每次将当前数加入到小的那个数中就能的到最优解。

首先有个很显然的结论，对于最后的两个数

有几个引理：

最终的两个数内部必然是按 $9\sim 0$ 的顺序排列。
这个很显然不加证明，能得到结论 $0$ 必然在两数的末尾。
所以为了方便我们可以先不考虑 $0$。
在只考虑 $1\sim 9$时，两数的长度差不会超过 $1$。
考虑用反证法：
记最终结果两数为 $a,b$ 有 $a>b,a=10x+y(1 \le y \le 9,x\ge10),len(a)-len(b)>1$。考虑将a末尾的 $y$ 加到 $b$ 后面，则有 $a’=x,b’=10b+y$。
$a’b’=x(10b+y)=10xb+xy,ab=10xb+y$。
所以 $a’b’>ab$。
与 $ab$ 最优矛盾，所以长度差不可能超过 $1$。
所以当总个数是偶数时最终两数等长，奇数时两数长度差 $1$（不考虑 $0$）。
那么当总个数是奇数时，我们不妨取一个 $0$ 出来，使总数变成偶数。
对于某一数字 $i(0 \le i \le 9)$，其在两数中出现的最高位最多差一位，最低为也最多差一位。
由 $2$ 不妨将总数设为 $2k$。
用反证法证明：
不妨设 $i$ 在两数 $A,B$ 中出现的最高位为 $x,y(x+1<y<k)$。
记 $A_j$ 表示数 $A$ 从第为往高位数第 $j$ 位的数字（从 $0$ 开始）。
由 $1$ 可知 $A_{x+1}>A_x$。
考虑将 $A_{x+1}$ 和 $B_y$ 交换。
则 $A’B’=(A+(B_y-A_{x+1})\times 10^{x+1})(B+(A_{x+1}-B_y)\times 10^y) $
$=AB+(A_{x+1}-B_y)\times(A\times10^y-B\times10^{x+1})$。
因为 $A_{x+1}>A_x=B_y,A\times10^{x+1}<B\times 10^{x+1}<B\times 10^y$。
所以 $A’B’>AB$。
与 $AB$ 最优矛盾。
所以位数不会差超过 $1$ 位。
最低位同理不多赘述。
如果 $A>B$，有唯一 $i$ 使得 $A_i>B_i$。
考虑反正法，如果存在 $j<i,A_j>B_j$。那么将 $A_j,B_j$ 交换。
$A’B’=(A+(B_j-A_j)\times 10^j)(B+(A_j-B_j)\times10^j)$
$=AB+(A_j-B_j)\times(A-B)\times10^j-(A_j-B_j)^2\times 10^{2j}$
$=AB+(A_j-B_j)((A-B)\times10^j-(A_j-B_j)\times10^{2j})$
$>AB+(A_j-B_j)((A-B)\times10^j-10^{2j+1})$
因为 $A_j>B_i$。
所以 $A-B\ge10^i$。
所以 $A’B’>AB+(A_j-B_j)(10{i-j-1})>AB$。
与 $AB$ 最优矛盾。

下面就按照上述四个要求构造即可。

最终结果即为开头给出的构造。

接下来考虑让某一数字的个数不同。

因为 $c_0>0$ 所以一定有一个数的末尾是 $0$。

所以我们只需将这个数除以 $2$，将另一个数乘 $2$ 即可。

因为首位必定是 $8/9$ 乘 $2$ 必然产生进位，除以 $2$ 必然不会退位，所以这么操作之后总位数会多 $1$，则必有一个数字的个数与给出的个数不同。

当然除以 $5$ 也行。甚至你可以将两个数卷起来。

并且由于两数形如 $99\cdots988\cdots8\cdots00\cdots0$。

可以将连续的 $i$ 看作 $\dfrac{10^k-1}{9}\times i$。

然后甚至可以手动把括号拆开。

Build

不难发现，每个小镇花费的价钱只与该小镇建了多少条公路有关，与和哪个小镇建的无关。而每个小镇修建的条数就是最后生成的途中该点的度数，记为 $du_i$。

所以我们不妨从每个小镇的角度进行求解。将每个小镇修建下一条公路的代价排序后取最小值。显然修建 $m$ 条道路，即 $\sum\limits_{i=1}^n du_i=2m$。所以只需取 $2m$ 次最小值即可。

上述过程可以用堆维护。

但是还没结束，还要满足图连通和没有自环两个条件。

图连通的一个显然的必要条件是 $\forall i \in [1,n],du_i>0$。

无自环的一个显然的必要条件是 $\forall i \in [1,n],du_i\le m$。

下面给出构造方案以证明充分性：

我们只需不断的将当前度数最小值的点连向度数最大值的点即可。

证明连通性

考虑当当前的度数最小值是 $1$ 时，连了这条边之后它将无法再和其它点连边。但是连了这条边之后，它将和当前的度数最大的点连通。

而之前和它连通的点（可能没有），也会间接的和剩下的点连通。

也就是说每个度数变为 $0$ 的点都会直接或间接的和当前剩下的度数不为 $0$ 的点连通。

所以最终这 $n$ 个点会连通。

证明无自环

考虑用反证法，假设最终会产生自环，即 $\exists i \in [1,n],du_i>0$。而由于总度数是偶数，每次连边也会使总度数减 $2$。所以 $du_i\ge 2$ 且 $ du_i \bmod 2=0$。

$i$ 会有两种情况：

$du_i$ 一直是最大值，那么意味着一直是将 $i$ 与其他点连边，即 $du_i>2m-du_i$，这与上面要求的 $du_i\le m$ 矛盾。
存在 $j$，满足在最开始时 $du_j>du_i$。那么当 $du_j$ 减到 $du_i$ 时，根据上述过程不难发现，在此之后会满足 $|du_i-du_j|\le 1$。而根据假设此时 $du_i-du_j\ge 2$。产生矛盾。

所以假设不成立，即最后不会产生自环。

时间复杂度 $O(m\log n)$

示例代码：

 1#define pli pair<ll,int>
 2const int N = 2e5 + 10;
 3int n, m, du;
 4ll ans;
 5struct P{
 6	int id, a, b, c, cnt;
 7	inline void rd(int i){id = i, cin >> a >> b >> c;}
 8	inline ll get(){cnt++; return (1ll * a * cnt + b) * cnt + c;}
 9} v[N];
10priority_queue<pli, vector<pli>, greater<pli>> q;
11pli now;
12inline bool cmp(P x, P y){return x.cnt > y.cnt;}
13int main()
14{
15	ios::sync_with_stdio(false);
16	cin >> n >> m, du = m << 1;
17	for(int i = 1; i <= n; ++i) v[i].rd(i);
18	
19	for(int i = 1; i <= n; ++i) ans += v[i].get();
20	du -= n;
21	
22	for(int i = 1; i <= n; ++i) q.push(make_pair(v[i].get(), i));
23	
24	while(du--)
25	{
26		now = q.top(), q.pop();
27		ans += now.first;
28		if(v[now.second].cnt == m){v[now.second].cnt++;continue;}
29		q.push(make_pair(v[now.second].get(), now.second));		
30	}
31	for(int i = 1; i <= n; i++) v[i].cnt--; 
32	
33	cout<<ans<<'\n';
34	
35	sort(v + 1, v + n  + 1, cmp);
36	int l = 1, r = n;
37	while(v[r].cnt == 0) r--;
38	while(l < r)
39	{
40		if(v[1].cnt == 1)break;
41		cout<<v[r].id<<' '<<v[l].id<<'\n';
42		v[r].cnt--, v[l].cnt--;
43		l++;
44		if(v[l].cnt <= v[1].cnt && v[1].cnt) l = 1;
45		if(!v[r].cnt) r--;
46		if(l == r && v[l].cnt)swap(v[l], v[1]), l = 1;
47	}
48	if(v[1].cnt)
49	{
50		for(int i = 2; i <= n; i++)
51			if(v[i].cnt)
52			{
53				cout<<v[i].id<<' '<<v[i-1].id<<"\n";
54				v[i].cnt--, v[i-1].cnt--;
55			}
56	}
57	return 0;
58}

赛时选手提供的爆标思路

同样只考虑每个点的度数，显然会有一个最大值，我们不妨直接二分这个最大值。然后可以用二次函数求根公式快速计算每个点选了多少次。然后判断总度数是否达到 $2m$ 且每个点度数仍符合上述条件即可。复杂度可以做到 $O(n\log V+m)$。

Mole

subtask1

纯暴力

$10\space pts$

subtask2

考虑 $dp$， $dp_{i,j,k}$ 表示在第 $i$ 位置，前面的 $j$ 个数取了 $k$ 次的答案。 $\Theta(n^3)$

$30\space pts$。

subtask3

考虑在 $1 \sim i-1$ 秒的基础上得到 $1 \sim i$ 秒的答案。

显然，$1 \sim i$ 的最优取法，必然包括 $1 \sim i-1$ 的取法。

我们有如下两种方式：

如果在 $i \sim i+l-1$ 中取最优，那么直接在第 $i$ 秒取它即可，对前 $i-1$ 秒的取法没有影响故仍取最优解最优。
将 $1 \sim i-1$ 秒的情况后面一段推迟一秒取，即将原本第 $i-1$ 取的数放到第 $i$ 秒取。这样我们就可以在前面某一个位置多取一个数。不妨令后移的左端点为 $l$，显然 $l$ 会有一个最小值的限制，即无法从很早的位置进行后移。但在这种情况下，假设我们取了 $val$(所有能取的数中最大的一个) 并将原本在 $val$ 后面的数全部推迟一秒取。那么有 $val$ 小于其后面所有数。不然在第 $i-1$ 秒时，我们就可以将 $val$ 后面小于它的一个数不取，用 $val$ 来代替那个数更优，这与当前取的数是 $i-1$ 秒时的最优解矛盾。

$\Theta(n^2)$，$60\space pts$

full task

考虑优化检验到 $\Theta(logn)$

考虑基于前一次推。对于每一轮检验，设 $f_n$ 为窗口右端到序列右端取的总次数（后缀和），$t_n$ 为窗口右端到 $n$ 至窗口离开序列的时间。

对于一种可行方案，当且仅当 $\forall i,f_n\le t_n$

充分性证明(口胡)：
假设 $f_n>t_n$
则在窗口离开之后 $a_i(n-L \le i \le n)$ 中必定有数没取，不合法。

必要性证明(口胡)： $\forall f_n$，
当其不大于 $t_n$ 并且方案不合法的时候，必定存在$f_x(x<n)>f_n$。

考虑 $f$ 的性质，
当 $f_n=0$ 时，直接在 $n$ 处扩展一位，即 $f_n=1$ （不存在要取的数时直接取走）
否则，$f_n←f_n+1$，并在下一个位置插入一次取数（相当于顺延直到找到0）

使用线段树维护区间加，并查集~~或线段树二分~~维护某位置后面第一个零。

假设插入一个数之后 $f_n>t_n$ 则无法插入，不合法。

维护存在性，设 $d_n=t_n-f_n$。

线段树初始化为 $t$，更新时区间减一，维护区间最小值，判断是否为负数。

考虑任意时间，对当前情况下的时间加一，将最后一位新加入的加进堆，
将 $t$ 的末 $L$ 位加一（末 $L$ 位可以向新的位置移动），在线段树中可以 $\Theta(logn)$。

由于每次加一处理完后都无法再次插入任何数，因此并查集维护的最后一个零其实就位于当前段末尾。

使用线段树和堆维护即可。

正常维护加一次取数即可，(时间轴上的每次移动最多取数一次)

和上面 subtask2 同理，中途被毙掉的数以后也不会选。

$\Theta(nlogn)$，$100\space pts$

示例代码:

 1#define ls (rt<<1)
 2#define rs (rt<<1|1)
 3#define ll long long
 4#define pii pair<int,int>
 5#define m_p make_pair
 6const int N=1e6+10;
 7int n,m,a[N],cnt;
 8int mn[N<<2],lim,tp;
 9ll ans;
10priority_queue<pii>q;
11void upd(int rt){return tp=min(mn[ls],mn[rs]),mn[ls]-=tp,mn[rs]-=tp,mn[rt]+=tp,void();}
12void change(int l,int r,int val)
13{
14	for(l+=lim-1,r+=lim+1;l^r^1;l>>=1,r>>=1,upd(l),upd(r))
15		(~l&1)&&(mn[l^1]+=val),(r&1)&&(mn[r^1]+=val);
16	for(;l^1;l>>=1)upd(l>>1);
17	return;
18}
19int query(int l,int r)
20{
21	int la=0,ra=0;
22	l+=lim,r+=lim;
23	if(l^r)
24		for(;l^r^1;l>>=1,r>>=1)
25			la+=mn[l],ra+=mn[r],
26			(~l&1)&&(la=min(la,mn[l^1])),
27			(r&1)&&(ra=min(ra,mn[r^1]));
28	int res=min(la+mn[l],ra+mn[r]);
29	for(;l^1;)res+=mn[l>>=1];
30	return res;
31}
32int main()
33{
34	m=read(),n=read();
35	for(int i=1;i<=n;i++)a[i]=read();
36	for(int i=1;i<m;i++)if(a[i]>0)q.push(m_p(a[i],i));
37	for(lim=1;lim<n;lim<<=1); 
38	for(int i=m;i<=n;i++)
39	{
40		if(a[i]>0)q.push(m_p(a[i],i));
41		change(i-m+1,i,1);
42		for(int l,r;q.size();)
43		{
44			l=q.top().second,q.pop(),r=i;
45			if(query(l,r)==0)continue;
46			change(l,r,-1),ans+=a[l],a[l]--;
47			if(a[l])q.push(m_p(a[l],l));
48			break;
49		}
50		writeL(ans,' ');
51	}
52	return 0;
53}

Water

显然这道题可以分成两个部分来计算，总方案数和所有方案的时间总数。

先考虑总方案数：

对于同一连通块，如果没有分支（任意位置放水都会使这一层全填满，如下图），很显然其方案数就是深度 $+1$（可以不放）。

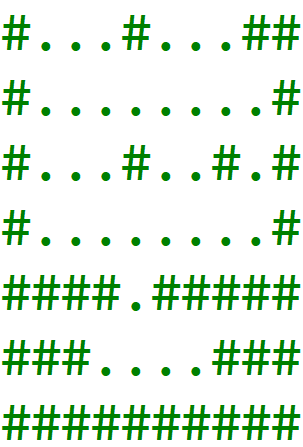
如果有分支，因为任意分支的方案不会互相影响，所以根据乘法原理不同分支的方案数直接乘起来即可，比如下图的方案数就应该是 $10$。

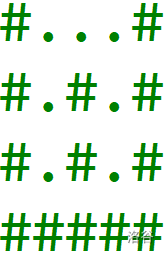
显然是否有分支可以用并查集来维护，记 $f_i$ 表示 $i$ 所对应连通块的方案数，当两个分支合并时，显然大的连通块方案数即 $f_x \times f_y +1$。

由于水因重力会下沉，所以很自然的就应该从下往上处理。对于每一层先将同层的连通块合并，再考虑从下一层更新过来。

若果发现相邻两点在该层是连通块但下一层和该点未连通，则可认为下层是一个新的分支，将其方案数乘到当前连通块。

在和下一层合并完后，还需再加上将水放在该层的一种方案。

对于最终仍未不连通的连通块，其方案之间仍是互不干扰的则需全部乘起来。

时间复杂度为 $O(n^2)$。

到此方案数就求完了，下面考虑求总时间。

考虑求出每种时间的方案数，最后在乘上时间。

记每个点的深度为这个点到其所在的连通块中最靠近顶部的点的距离。

对于同一连通块，该块所需时间为该方案下所有水中最浅的水的深度。

而对于不同连通块，最终时间即为所有连通块中时间的最大值。

显然，对于某一深度求出答案并不是很容易，考虑容斥，如果已知前缀和，那么直接相减即为每一深度的答案。

那么如何来求前缀和，由于最终各块之间是取最大值，故只需知道各块之间方案的前缀和，相乘即可。

现在问题转化为求各连通块各深度方案数的前缀和。

类比求总方案数，由于总方案数是从下往上求的，故 $f_i$ 就表示该连通块深度大于等于目前深度的方案数，

但考虑对于每个最终连通块，在每个深度可能有多个分支，需要将每个分支的深度都乘起来（可以对于每个连通块开一个 $\tt{vector}$，每个 $\tt{vector}$ 的大小为该块最大深度 $+1$）。

现在就得到了每个连通块的后缀和，前缀和只需用总和减去后缀和。

这个问题就解决了。

~~但万恶的出题人卡了空间~~有如下几种解决方式：

$\tt{vector}$ 改成数组，并手动分配每一块的空间。
把只有一层的连通块忽略，这样连通块的个数最多为 $\dfrac{n^2}{4}$。
并查集数组可以循环使用。
在预处理每个点的深度时用 $\tt{bfs}$ 并且对于每一行中连续的一段点只入队一次。

综上：时间复杂度为 $O(n^2)$、空间复杂度为 $O(n^2)$。

 1const int N=5001,mod=998244353;
 2int n,m,ans1=1,cnt,sum[N],ans2,mul[N],mx,dep,fir[N*N/4],Tm[N*N/2],id[N*N],f[N<<1],fa[N<<1];
 3queue<int>q;
 4bool s[N][N];
 5#define get_id(x,y) (m*(x-1)+y)
 6inline int get(int x){return fa[x]==x?x:fa[x]=get(fa[x]);}
 7inline int bfs(int &i,int &j,int ct)
 8{
 9	int t=1,h=0,x=i,y=j,k,kk,*id_,*id__,dep_=ct,l,r,mx=0;
10	q.push(i),Tm[0]=j;
11	for(r=y,id_=id+get_id(i,j);s[x][r];++id_,++r)*id_=dep_;
12	for(l=y,id_=id+get_id(i,j);s[x][l];--id_,--l)*id_=dep_;
13	for(;h!=t;h++)
14	{
15		x=q.front(),q.pop(),y=Tm[h],mx=max(mx,x-i),dep_=ct+x-i;
16		for(r=y;s[x][r];++r);
17		for(l=y-1;s[x][l];--l);
18		for(k=l+1,id_=id+get_id(x,k);k<r;++id_,++k)
19		{
20			if(s[x-1][k]&&*(id_-m)==-1)
21			{
22				q.push(x-1),Tm[t]=k,t++;
23				for(id__=id_-m,kk=k;s[x-1][kk];--id__,--kk)*id__=dep_-1;
24				for(id__=id_-m,kk=k;s[x-1][kk];++id__,++kk)*id__=dep_-1;
25			}
26			if(s[x+1][k]&&*(id_+m)==-1)
27			{
28				q.push(x+1),Tm[t]=k,t++;
29				for(id__=id_+m,kk=k;s[x+1][kk];--id__,--kk)*id__=dep_+1;
30				for(id__=id_+m,kk=k;s[x+1][kk];++id__,++kk)*id__=dep_+1;
31			}
32		}
33	}
34	if(mx==0)for(int k=l;k<=r;k++)s[x][k]=0;
35	return mx;
36}
37inline int ksm(int x,int p)
38{
39	int res=1;
40	for(;p;p>>=1,x=1ll*x*x%mod)if(p&1)res=1ll*x*res%mod;
41	return res;
42}
43int main()
44{
45	n=read(),m=read();
46	for(int i=1,opt;i<=n;i++)
47	{
48		for(opt=G();opt!='.'&&opt!='#';opt=G());
49		for(int j=2;j<=m;j++)s[i][j]=G()-'#';
50	}
51	memset(id+1,-1,n*m*sizeof(int));
52	
53	//标记每个连通块的点并分配空间和去除深度为1的连通块 
54	for(int i=1,*id_=id+1,now;i<=n;i++)
55		for(int j=1;j<=m;++j,++id_)
56			if(*id_==-1&&s[i][j])
57				++cnt,now=bfs(i,j,fir[cnt]=fir[cnt-1]+dep+1),cnt-=(now==0),dep=now?now:dep;
58	
59	for(int i=fir[cnt]+dep;i>=1;--i)Tm[i]=1;
60	fir[cnt+1]=fir[cnt]+dep+1;
61	
62	//统计总方案数和每一连通块的方案后缀和 
63	for(int i=n-1;i>=1;i--)
64	{
65		for(int j=2;j<m;j++)fa[j]=(s[i][j-1]?fa[j-1]:j),f[j]=1;
66		for(int j=2,fx,fy;j<m;j++)
67			if(s[i][j]&&s[i+1][j]&&(fx=get(j))!=(fy=get(j+m)))
68					f[fx]=1ll*f[fx]*f[fy]%mod,fa[fy]=fx;
69		for(int j=2,*id_=id+get_id(i,j);j<m;++id_,++j)
70			if(s[i][j]&&fa[j]==j)
71				f[j]++,Tm[*id_]=1ll*Tm[*id_]*f[j]%mod;
72		for(int j=2;j<m;j++)fa[j+m]=fa[j]+m;
73		memcpy(f+m+1,f+1,sizeof(int)*m);
74	}
75	for(int i=0;i<=n;i++)sum[i]=mul[i]=1;
76	
77	//合并各个连通块的答案 
78	for(int i=1,sm,sz,*T;i<=cnt;i++)
79	{
80		T=Tm+fir[i],sz=fir[i+1]-fir[i]-1,sm=*T;
81		ans1=1ll*sm*ans1%mod,mx=max(mx,sz);
82		mul[sz+1]=1ll*mul[sz+1]*sm%mod,sum[sz]=1ll*sum[sz]*sm%mod;
83		for(int j=0;j<sz;j++)sum[j]=1ll*sum[j]*(sm+1-*(T+j+1))%mod;
84	}
85	for(int i=1;i<=mx;i++)mul[i]=1ll*mul[i]*mul[i-1]%mod,sum[i]=1ll*sum[i]*mul[i]%mod;
86	for(int i=1;i<=mx;i++)ans2=(1ll*(sum[i]-sum[i-1])*i+ans2)%mod;
87	printf("%lld",(1ll*ans2*ksm(ans1,mod-2)%mod+mod)%mod);
88	return 0;
89}

Competition

根据题意，积极性的期望就是每种方案的积极性 $\times$ 这种方案的概率。

形式化的，我们记 $P_k$ 表示最终有 $k$ 个人达到分数线的概率，$F_k$ 表示给 $k$ 个人发奖品的方案数，$val_k$ 表示给 $k$ 个人发奖品所有方案的积极性之和。

那么对于一种发给 $k$ 个人奖品的方案其概率为 $\dfrac{P_k}{F_k}$。

则最终期望 $E=\sum\limits_{k=0}^n \dfrac{P_k\times val_k}{F_k}$。

下面考虑分别求出 $P_k$，$F_k$，$val_k$。

$P_k$：

显然可以 $O(n^2)$ 进行 $\tt{DP}$。记 $f_{i,j}$ 表示前 $i$ 个人中有 $j$ 个人达到分数线的概率。那么有 $f_{0,0}=1$，$f_{i,j}=f_{i-1,j}\times (1-p_i)+f_{i-1,j-1}\times p_i$。

但这个复杂度显然不能接受。套路性的，我们考虑答案的生成函数 $\sum\limits_{k=0}^n P_kx^k$。而每个人的生成函数即为 $1-p_i+p_ix$。

则 $\sum\limits_{k=0}^n P_kx^k = \prod\limits_{i=1}^n (1-p_i+p_ix)$。

普通分治乘法就可以解决这个问题。

$F_k$：

有 $O((A+B)n^2)$ 的 $\tt{DP}$，记 $f_{i,j}$ 表示用前 $i$ 个奖品发给 $j$ 个人的方案数。

枚举第 $i$ 个奖品用了多少个和发给多少人。

对于 $\text{A}$ 类奖品有转移 $f_{i,j}=\sum\limits_{k\text{为偶数}}^j f_{i-1,j-k}\times \binom{j}{k}$。

对于 $\text{B}$ 类奖品有转移 $f_{i,j}=\sum\limits_{k\text{为奇数}}^j f_{i-1,j-k}\times \binom{j}{k}$。

不难发现转移过程类似卷积，但不完全一样。套路的将组合数写成阶乘的形式。

即对于 $\text{A}$ 类奖品有转移 $f_{i,j}=\sum\limits_{k\text{为偶数}}^j f_{i-1,j-k}\times \dfrac{j!}{k!\times (j-k)!}=j!\times \sum\limits_{k\text{为偶数}}^j \dfrac{f_{i-1,j-k}}{(j-k)!}\times \dfrac{1}{k!}$。

不考虑 $j!$ 这个式子就可以用 $\tt{NTT}$ 优化了。

对于 $\text{B}$ 类奖品也是一样的。复杂度 $O((A+B)n\log n)$。

不难发现每次卷的多项式都是一样的。

对于 $\text{A}$ 类，每个奖品的生成函数均为 $1+\dfrac{x^2}{2!}+\dfrac{x^4}{4!}\cdots$。

即最终的结果即为 $(1+\dfrac{x^2}{2!}+\dfrac{x^4}{4!}\cdots)^A$。

多项式快速幂即可。

对于 $\text{B}$ 类，每个奖品的生成函数为 $\dfrac{x}{1!}+\dfrac{x^3}{3!}\cdots$。

而 $(\dfrac{x}{1!}+\dfrac{x^3}{3!}\cdots)^B$ 由于常数项不为 $1$，有两种处理方式：

转化为 $x^B(\dfrac{1}{1!}+\dfrac{x^2}{3!}\cdots)^B$ 直接快速幂即可。
多项式幂函数（加强版）。

最后再将 $\text{A}$，$\text{B}$ 两类的方案数卷起来乘上 $k!$ 就可以得到 $F_k$。

复杂度 $O(n\log n)$。

$val_k$：

$\tt{DP}$ 做法及优化和求方案数一样，只需多乘一个价值。

对于 $\text{B}$ 类，每种奖品价值的生成函数为 $b_i(\dfrac{x}{1!}+\dfrac{x^3}{3!}\cdots)$。

则 $\text{B}$ 类的方案价值生成函数即为 $(\dfrac{x}{1!}+\dfrac{x^3}{3!}\cdots)^B \prod\limits_{i=1}^B b_i$。

将之前求过的方案数乘上 $\prod\limits_{i=1}^B b_i$ 即可。

对于 $\text{A}$ 类，每种奖品价值的生成函数为 $1+\dfrac{a_i}{2!}x^2+\dfrac{a_i}{4!}x^4\cdots$。

这个东西显然不能用快速幂做。考虑其指数型生成函数 $\tt{EGF}$。

由 $e^x=\sum\limits_{k=0}^{\infty} \dfrac{x^k}{k!}$，$e^{-x}=\sum\limits_{k=0}^{\infty} (-1)^k\dfrac{x^k}{k!}$。

则 $1+\dfrac{x^2}{2!}+\dfrac{x^4}{4!}\cdots=\dfrac{e^x+e^{-x}}{2}$。

$1+\dfrac{a_i}{2!}x^2+\dfrac{a_i}{4!}x^4\cdots=a_i(\dfrac{e^x+e^{-x}}{2}-1)+1$。

$\prod\limits_{i=1}^A (1+\dfrac{a_i}{2!}x^2+\dfrac{a_i}{4!}x^4\cdots)=\prod\limits_{i=1}^A (a_i(\dfrac{e^x+e^{-x}}{2}-1)+1)$。

考虑将上述式子展开后，再将 $e^{kx}$ 泰勒展开回普通型生成函数。

为了方便处理，先将 $e^{-x}$ 提出来。

$\prod\limits_{i=1}^A (a_i(\dfrac{e^x+e^{-x}}{2}-1)+1)=e^{-Ax}\prod\limits_{i=1}^A(\dfrac{a_i}{2}e^{2x}+(1-a_i)e^x+\dfrac{a_i}{2})$。

将 $e^x$ 看成 $x$。用分治乘法将其展开。得到一个形如 $\sum\limits_{i=0}^{2A} c_ie^{i-A}$ 的多项式。

接下来就是将 $e^{kx}$ 泰勒展开。

即对于每个 $k\in[1,n]$，求出 $\sum\limits_{i=0}^{2A}c_i(i-A)^k$。

当 $c_i=1$ 时，就是直接求自然数幂和（可参考calc加强版或[THUPC2017] 小 L 的计算题）。

对于任意情况：

同样考虑最终答案的生成函数 $G(x)=\sum\limits_{k=0}^{\infty}x^k\sum\limits_{i=0}^{2A}c_i(i-A)^k$。

因为 $\sum\limits_{k=0}^{\infty}a^kx^k=\dfrac{1}{1-ax}$。

所以 $G(x)=\sum\limits_{i=0}^{2A}\dfrac{c_i}{1-(i-A)x}$。

直接通分：

$$G(x)=\dfrac{\sum\limits_{i=0}^{2A}c_i\prod\limits_{j=0,j\ne i}^{2A}(1-(j-A)x)}{\prod\limits_{i=0}^{2A}{(1-(i-A)x)}}$$

同样考虑用分治求解上述式子。

我们记 $A(l,r)=\sum\limits_{i=l}^{r}c_i\prod\limits_{j=l,j\ne i}^r(1-(j-A)x)$，$B(l,r)=\prod\limits_{i=l}^{r}{(1-(i-A)x)}$。

不难发现 $A(l,r)=A(l,mid)\times B(mid+1,r)+A(mid+1,r)\times B(l,mid)$，$B(l,r)=B(l,mid)\times B(mid+1,r)$。

直接分治即可。复杂度 $O(n\log^2n)$。

而之前求方案数同样可以考虑用上述分治方法完成。并且由于多项式快速幂的大常数，两者的效率差不多。

综上最终的复杂度为 $O(n\log^2n)$。